Searching for a shell

The Sokhotski-Plemelj Formula

Math 

The Sokhostski-Plemelj formula is the following relation:

lim⁡ϵ→01x±iϵ=P1x∓iπδ(x),(1)\lim _{\epsilon \rightarrow 0} \frac{1}{x \pm i \epsilon} = \mathcal{P} \frac{1}{x} \mp i \pi \delta(x), \tag{1}

where $\epsilon$ is an positive infinitesimal real number and $\mathcal{P}$ means the Cauchy principal value. Eq. 1 doesn’t make any sense until we’ve plug a function ($f(x)$) in and integrating both sides. (That’s why Eq. q is also called distribution equilty). Also, to make the integration convergent, we need $f(x) \rightarrow 0$ faster than $1/x \rightarrow 0$ as $x \rightarrow \pm \infty$. Doing that, gives us:

lim⁡ϵ→0∫−∞∞f(x)dxx±iϵ=P∫−∞∞f(x)dxx∓iπf(0),(2)\lim _{\epsilon \rightarrow 0} \int_{-\infty}^{\infty} \frac{f(x) d x}{x \pm i \epsilon}=\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x) d x}{x} \mp i \pi f(0), \tag{2}

and now we can finally write the principle value as:

P∫∞∞f(x)xdx≡lim⁡δ→0{∫−∞−δf(x)dxx+∫δ∞f(x)dxx}.\mathcal{P} \int_\infty^\infty \frac{f(x)}{x} dx \equiv \lim_{\delta \rightarrow 0} \left \{ \int_{-\infty}^{-\delta} \frac{f(x)dx}{x} + \int_{\delta}^{\infty} \frac{f(x)dx}{x} \right \}.

Alternatively, Eq. 1 can be generalized by substituting $x$ with $x-x_0$:

lim⁡ϵ→01x−x0±iϵ=P1x−x0∓iπδ(x−x0),(3)\lim _{\epsilon \rightarrow 0} \frac{1}{x-x_0 \pm i \epsilon} = \mathcal{P} \frac{1}{x-x_0} \mp i \pi \delta(x-x_0), \tag{3}

and Eq. 2 would turn to:

lim⁡ϵ→0∫−∞∞f(x)dxx−x0±iϵ=P∫−∞∞f(x)dxx−x0∓iπf(x0),(4)\lim _{\epsilon \rightarrow 0} \int_{-\infty}^{\infty} \frac{f(x) d x}{x-x_0 \pm i \epsilon}=\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x) d x}{x-x_0} \mp i \pi f(x_0), \tag{4}

where:

P∫−∞∞f(x)dxx−x0≡lim⁡δ→0{∫−∞x0−δf(x)dxx−x0+∫x0+δ∞f(x)dxx−x0}\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x) d x}{x-x_{0}} \equiv \lim _{\delta \rightarrow 0}\left\{\int_{-\infty}^{x_{0}-\delta} \frac{f(x) d x}{x-x_{0}}+\int_{x_{0}+\delta}^{\infty} \frac{f(x) d x}{x-x_{0}}\right\}

Derivation

To prove the Sokhotski-Plemelj formula, we first need to consider contour integration of the integrand $f(x)/x$ over the following coutour:

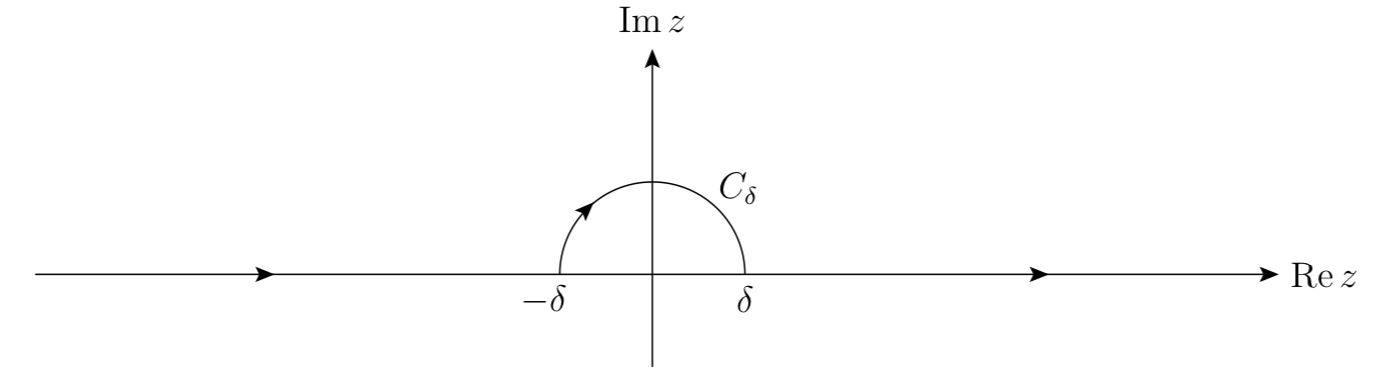
The contour $C$ is along the real axis from $-\infty$ to $-\delta$, followed by a semicircle $C_\delta$ in the upper plane with a radius of $\delta > 0$, and followed by anoter straight contour along the real axis from $\delta$ to $\infty$.

This integration can be written as:

lim⁡δ→0∫Cf(x)xdx=lim⁡δ→0{∫−∞−δf(x)dxx+∫δ∞f(x)dxx+∫Cδf(x)xdx}=P∫−∞∞f(x)x+lim⁡δ→0∫Cδf(x)xdx,(5)\begin{aligned} \lim _{\delta \rightarrow 0}\int_{C} \frac{f(x)}{x} d x &= \lim _{\delta \rightarrow 0}\left\{\int_{-\infty}^{-\delta} \frac{f(x) d x}{x}+\int_{\delta}^{\infty} \frac{f(x) d x}{x}+\int_{C_{\delta}} \frac{f(x)}{x} d x\right\} \\ &=\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x)}{x}+\lim_{\delta \rightarrow 0}\int_{C_{\delta}} \frac{f(x)}{x} d x, \end{aligned} \tag{5}

In the limit of $\delta \rightarrow 0$ we can approximate $f(x) \approx f(0)$ in the second term. Taking the analytical form of the semicircle, we can replace $x$ in the secon term with $x=\delta e^{i\theta}$ for $0\leq \theta \leq \pi$. Doing that, the second term in Eq. 5 turns into:

lim⁡δ→0∫Cδf(x)xdx=f(0)lim⁡δ→0∫π0iδeiθδeiθdθ=−iπf(0)\lim _{\delta \rightarrow 0} \int_{C_{\delta}} \frac{f(x)}{x} d x=f(0) \lim _{\delta \rightarrow 0} \int_{\pi}^{0} \frac{i \delta e^{i \theta}}{\delta e^{i \theta}} d \theta=-i \pi f(0)

so that Eq. 5 is now:

lim⁡δ→0∫Cf(x)xdx=P∫−∞∞f(x)xdx−iπf(0)(6)\lim _{\delta \rightarrow 0}\int_{C} \frac{f(x)}{x} d x=\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x)}{x}dx -i \pi f(0) \tag{6}

We see that Eq. 6 looks pretty similar to Eq. 4 with the only difference being $i\epsilon$ in the denominator and the integration over the real axis instead of over the contour.

It turns out, we can deform the contour integration over $C$ to $C’$ that consists of a straight line that runs from $-\infty + i\epsilon$ to $\infty + i\epsilon$, where $\epsilon$ is a positive infinitesimal of the same order of magnitude as the radius of the semicircle $\delta$:

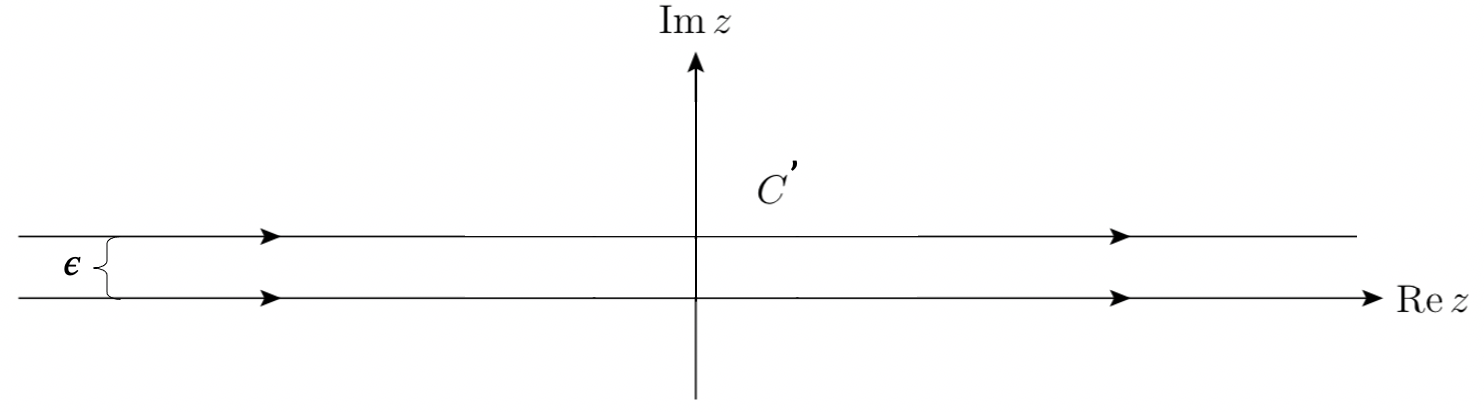
as long as $f(x)$ has no singularities in an infinitesimal neighborhood around the real axis. We can write:

lim⁡δ→0∫Cf(x)xdx=lim⁡ϵ→0∫C′f(x)xdx=lim⁡ϵ→0∫−∞+iϵ∞+iϵf(x)xdx=lim⁡ϵ→0∫−∞∞f(y+iϵ)y+iϵdy.(7)\lim _{\delta \rightarrow 0}\int_{C} \frac{f(x)}{x} d x= \lim _{\epsilon\rightarrow 0}\int_{C'} \frac{f(x)}{x} d x = \lim_{\epsilon \rightarrow 0}\int_{-\infty+i \epsilon}^{\infty+i \epsilon} \frac{f(x)}{x} d x=\lim_{\epsilon \rightarrow 0}\int_{-\infty}^{\infty} \frac{f(y+i \epsilon)}{y+i \epsilon} d y. \tag{7}

Since $\epsilon$ is infinitesimal, we can approximate $f(y+i\epsilon) \approx f(y)$. Thus, Eq. 7 can be written as:

lim⁡δ→0∫Cf(x)xdx=lim⁡ϵ→0∫−∞∞f(x)x+iϵdx,\lim _{\delta \rightarrow 0}\int_{C} \frac{f(x)}{x} d x=\lim_{\epsilon \rightarrow 0} \int_{-\infty}^{\infty} \frac{f(x)}{x+i \epsilon} d x,

and Eq. 6 can be written as:

lim⁡ϵ→0∫−∞∞f(x)x+iϵdx=P∫−∞∞f(x)xdx−iπf(0)(8)\lim_{\epsilon \rightarrow 0}\int_{-\infty}^{\infty} \frac{f(x)}{x+i \epsilon} d x=\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x)}{x}dx -i \pi f(0) \tag{8}

We can also take the complex conjugate of the resulting equation, and get:

lim⁡ϵ→0∫−∞∞f(x)x−iϵdx=P∫−∞∞f(x)xdx+iπf(0)(9)\lim_{\epsilon \rightarrow 0}\int_{-\infty}^{\infty} \frac{f(x)}{x-i \epsilon} d x=\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x)}{x} dx+i \pi f(0) \tag{9}

So that, in general, we get:

lim⁡ϵ→0∫−∞∞f(x)x±iϵdx=P∫−∞∞f(x)xdx∓iπf(0),(10)\lim_{\epsilon \rightarrow 0}\int_{-\infty}^{\infty} \frac{f(x)}{x\pm i \epsilon} d x=\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x)}{x} dx \mp i \pi f(0), \tag{10}

which is exactly the same as Eq. 2.

Reference: :link:UCSC-Physics 215

Author | Chengcheng Xiao

Currently a postdoctoral research associate at Imperial College London. Predicting electron behaviour since 2016.