Read
Read
Flavour 1
In this flavour, we first construct a real-space Hamiltonian and then Fourier transform it to reciprocal space to get the band structrue.
Steps to solve real-space TB hamiltonian
write real-space Hamiltonian.
transform the real-space Hamiltonian to reciprocal space.
change one of the exponential $e^{ikr}$ to $e^{ik(r-r’)} \cdot e^{ikr’}$.
use definition of the delta function: $\delta(k,k’) = \frac{1}{N} \sum_j e^{i(k-k’)r_i}$.
Using ladder operator in reciprocal space as basis and write the Hamiltonian in matrix form.
1D atomic chain
The real space Hamiltonian (assuming only nearest-neighbor hoppings):
H = − t ∑ i ( a i † a i + 1 + a i + 1 † a i ) . (1) H = -t \sum_i (a_i^\dagger a_{i+1} + a_{i+1}^\dagger a_{i}).
\tag{1} H = − t i ∑ ( a i † a i + 1 + a i + 1 † a i ) . ( 1 ) Remember that:
a i † = 1 N ∑ k e − i k r i a k † a i = 1 N ∑ k e i k r i a k , (2) \begin{aligned}
a_i^\dagger &= \frac{1}{\sqrt{N}} \sum_{k} e^{-ikr_i} a_k^\dagger\\
a_i &= \frac{1}{\sqrt{N}} \sum_{k} e^{ikr_i} a_k,
\end{aligned}
\tag{2} a i † a i = N 1 k ∑ e − ik r i a k † = N 1 k ∑ e ik r i a k , ( 2 ) so that:
H ^ = − t N ∑ i ( ∑ k e − i k r i a k † ∑ k ′ e i k ′ r i + 1 a k + ∑ k e − i k r i + 1 a k † ∑ k ′ e i k ′ r i a k ) (3) \hat H = -\frac{t}{N} \sum_i (\sum_k e^{-ikr_i} a_k^\dagger \sum_k' e^{ik'r_{i+1}}a_k + \sum_k e^{-ikr_{i+1}} a_k^\dagger \sum_k' e^{ik'r_{i}}a_k)
\tag{3} H ^ = − N t i ∑ ( k ∑ e − ik r i a k † k ∑ ′ e i k ′ r i + 1 a k + k ∑ e − ik r i + 1 a k † k ∑ ′ e i k ′ r i a k ) ( 3 ) next, we replace $e^{ik’r_{i+1}}$ and $e^{ik’r_i}$ with $e^{ik’(r_{i+1}-r_i)}\cdot e^{ik’(r_i)}$ and $e^{ik’(r_i-r_{i+1})}\cdot e^{ik’(r_{i+1})}$, respectively.
H ^ = − t N ∑ i ( ∑ k e − i k r i a k † ∑ k ′ e i k ′ r i + 1 a k + ∑ k e − i k r i + 1 a k † ∑ k ′ e i k ′ r i a k ) = − t N ∑ i [ ∑ k e − i k r i a k † ∑ k ′ e i k ′ ( r i + 1 − r i ) ⋅ e i k ′ ( r i ) a k + ∑ k e − i k r i + 1 a k † ∑ k ′ e i k ′ ( r i − r i + 1 ) e i k ′ r i + 1 a k ] = − t N ∑ i [ ∑ k k ′ e i ( k ′ − k ) r i e i k ′ ( r i + 1 − r i ) a k † a k + ∑ k k ′ e i ( k ′ − k ) r i e i k ′ ( r i − r i + 1 ) a k † a k ] = − t N { ∑ k k ′ [ ∑ i e i ( k ′ − k ) r i ] e i k ′ ( r i + 1 − r i ) a k † a k + ∑ k k ′ [ ∑ i e i ( k ′ − k ) r i ] e − i k ′ ( r i + 1 − r i ) a k † a k } = − t N [ ∑ k k ′ N δ ( k , k ′ ) e i k ′ ( r i + 1 − r i ) a k † a k + ∑ k k ′ N δ ( k , k ′ ) e − i k ′ ( r i + 1 − r i ) a k † a k ] = − t [ ∑ k e i k ( r i + 1 − r i ) a k † a k + ∑ k e − i k ( r i + 1 − r i ) a k † a k ] = − t [ ∑ k e i k ( r i + 1 − r i ) + ∑ k e − i k ( r i + 1 − r i ) ] a k † a k (4) \begin{align*}
\hat{H} &= -\frac{t}{N} \sum_i (\sum_k e^{-ikr_i} a_k^\dagger \sum_{k'} e^{ik'r_{i+1}}a_k + \sum_k e^{-ikr_{i+1}} a_k^\dagger \sum_{k'} e^{ik'r_{i}}a_k) \\
&\begin{aligned}
= -\frac{t}{N} & \sum_i [ \sum_k e^{-ikr_i} a_k^\dagger \sum_{k'} e^{ik'(r_{i+1}-r_i)}\cdot e^{ik'(r_i)} a_k \\
&+ \sum_k e^{-ikr_{i+1}} a_k^\dagger \sum_{k'} e^{ik'(r_{i}-r_{i+1})} e^{ik'r_{i+1}} a_k ]
\end{aligned}\\
&= -\frac{t}{N} \sum_i [\sum_{kk'} e^{i(k'-k)r_i} e^{ik'(r_{i+1}-r_i)} a_k^\dagger a_k + \sum_{kk'} e^{i(k'-k)r_i} e^{ik'(r_{i}-r_{i+1})} a_k^\dagger a_k] \\
&= -\frac{t}{N} \{ \sum_{kk'} [\sum_i e^{i(k'-k)r_i}] e^{ik'(r_{i+1}-r_i)} a_k^\dagger a_k + \sum_{kk'} [\sum_i e^{i(k'-k)r_i}] e^{-ik'(r_{i+1}-r_{i})} a_k^\dagger a_k \} \\
&= -\frac{t}{N} [ \sum_{kk'} N\delta(k,k') e^{ik'(r_{i+1}-r_i)} a_k^\dagger a_k + \sum_{kk'} N\delta(k,k') e^{-ik'(r_{i+1}-r_{i})} a_k^\dagger a_k] \\
&= -t [\sum_{k} e^{ik(r_{i+1}-r_i)} a_k^\dagger a_k + \sum_k e^{-ik(r_{i+1}-r_{i})} a_k^\dagger a_k] \\
&= -t [\sum_{k} e^{ik(r_{i+1}-r_i)} + \sum_k e^{-ik(r_{i+1}-r_{i})}] a_k^\dagger a_k \\
\end{align*}
\tag{4} H ^ = − N t i ∑ ( k ∑ e − ik r i a k † k ′ ∑ e i k ′ r i + 1 a k + k ∑ e − ik r i + 1 a k † k ′ ∑ e i k ′ r i a k ) = − N t i ∑ [ k ∑ e − ik r i a k † k ′ ∑ e i k ′ ( r i + 1 − r i ) ⋅ e i k ′ ( r i ) a k + k ∑ e − ik r i + 1 a k † k ′ ∑ e i k ′ ( r i − r i + 1 ) e i k ′ r i + 1 a k ] = − N t i ∑ [ k k ′ ∑ e i ( k ′ − k ) r i e i k ′ ( r i + 1 − r i ) a k † a k + k k ′ ∑ e i ( k ′ − k ) r i e i k ′ ( r i − r i + 1 ) a k † a k ] = − N t { k k ′ ∑ [ i ∑ e i ( k ′ − k ) r i ] e i k ′ ( r i + 1 − r i ) a k † a k + k k ′ ∑ [ i ∑ e i ( k ′ − k ) r i ] e − i k ′ ( r i + 1 − r i ) a k † a k } = − N t [ k k ′ ∑ N δ ( k , k ′ ) e i k ′ ( r i + 1 − r i ) a k † a k + k k ′ ∑ N δ ( k , k ′ ) e − i k ′ ( r i + 1 − r i ) a k † a k ] = − t [ k ∑ e ik ( r i + 1 − r i ) a k † a k + k ∑ e − ik ( r i + 1 − r i ) a k † a k ] = − t [ k ∑ e ik ( r i + 1 − r i ) + k ∑ e − ik ( r i + 1 − r i ) ] a k † a k ( 4 ) For each k point:
H ^ = − t [ e i k ( r i + 1 − r i ) + e − i k ( r i + 1 − r i ) ] a k † a k = − 2 t cos ( k [ r i + 1 − r i ] ) a k † a k (5) \begin{aligned}
\hat{H} &= -t[e^{ik(r_{i+1}-r_i)}+e^{-ik(r_{i+1}-r_{i})}] a_k^\dagger a_k\\
&= -2t\cos(k[r_{i+1}-r_i]) a_k^\dagger a_k
\end{aligned}
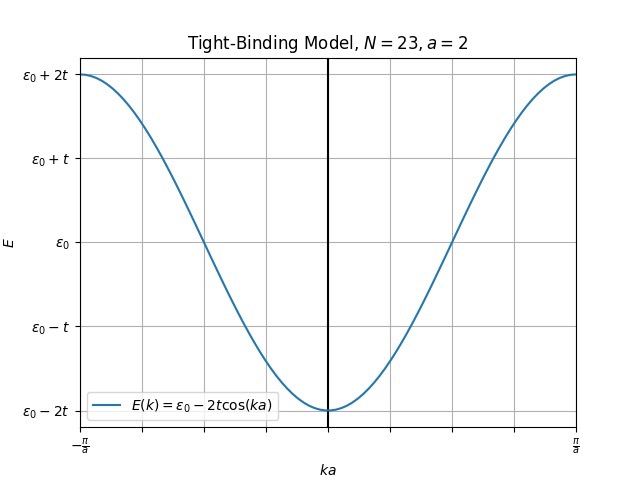
\tag{5} H ^ = − t [ e ik ( r i + 1 − r i ) + e − ik ( r i + 1 − r i ) ] a k † a k = − 2 t cos ( k [ r i + 1 − r i ]) a k † a k ( 5 ) so that the Hamiltonian matrix for 1D atomic chain is a single 1X1 matrix and the dispersion is a simple cos wave:
− 2 t cos ( k [ r i + 1 − r i ] ) = − 2 t cos ( k Δ ) (7) -2t\cos(k[r_{i+1}-r_i]) = -2t\cos(k\Delta)
\tag{7} − 2 t cos ( k [ r i + 1 − r i ]) = − 2 t cos ( k Δ ) ( 7 ) where $\Delta$ is the cell length.
and it looks like:
Since this is a 1X1 matrix, the basis it self is the eigenvector, we can revert it back to real-space by inverse FT:
a k ( r ) = 1 N ∑ j e i k r j a j ( r ) (8) a_k(r) = \frac{1}{\sqrt{N}} \sum_j e^{ikr_j} a_j(r)
\tag{8} a k ( r ) = N 1 j ∑ e ik r j a j ( r ) ( 8 ) 1D di-atomic chain
The Hamiltionian of this model can be written as:
H = − t ∑ i ( a i † b i + b i † a i + b i − 1 † a i + a i † b i − 1 ) (9) H = -t \sum_i (a^\dagger_i b_i + b^\dagger_i a_i + b_{i-1}^\dagger a_i + a_i^\dagger b_{i-1})
\tag{9} H = − t i ∑ ( a i † b i + b i † a i + b i − 1 † a i + a i † b i − 1 ) ( 9 ) Note : for di-atomic chain, only 4 hoppings are needed since there are only two bonds inside one unitcell.
Transform this Hamiltonian into reciprocal space:
H ^ = − t ∑ i ( a i † b i + b i † a i + b i − 1 † a i + a i † b i − 1 ) = − t N ∑ i ( ∑ k e − i k r i a a k † ∑ k ′ e i k r i b b k + ∑ k e − i k r i b b k † ∑ k ′ e i k r i a a k + ∑ k e − i k r i − 1 b b k † ∑ k ′ e i k r i a a k + ∑ k e − i k r i a a k † ∑ k ′ e i k r i − 1 b b k ) = − t [ ∑ k e i k ( r i b − r i a ) a k † b k + ∑ k e − i k ( r i b − r i a ) b k † a k + ∑ k e i k ( r i a − r i − 1 b ) b k † a k + ∑ k e − i k ( r i a − r i − 1 b ) a k † b k ] = − t [ ∑ k e i k ( r i a − r i − 1 b ) + e − i k ( r i b − r i a ) ] b k † a k − t [ ∑ k e i k ( r i b − r i a ) + e − i k ( r i a − r i − 1 b ) ] a k † b k = ∑ k 2 cos ( k Δ ) b k † a k + ∑ k 2 cos ( k Δ ) a k † b k (10) \begin{aligned}
\hat{H} &= -t \sum_i (a^\dagger_i b_i + b^\dagger_i a_i + b_{i-1}^\dagger a_i + a_i^\dagger b_{i-1})\\
&\begin{aligned}
= -\frac{t}{N} &\sum_i (\sum_k e^{-ikr^a_{i}} a^\dagger_k \sum_{k'} e^{ikr^b_{i}} b_k + \sum_k e^{-ikr^b_{i}} b^\dagger_k \sum_{k'} e^{ikr^a_{i}} a_k \\
&+ \sum_k e^{-ikr^b_{i-1}} b^\dagger_k \sum_{k'} e^{ikr^a_{i}} a_k + \sum_k e^{-ikr^a_{i}} a^\dagger_k \sum_{k'} e^{ikr^b_{i-1}} b_k)
\end{aligned}\\
&\begin{aligned}
= -t [ &\sum_k e^{ik(r^b_i - r^a_i)} a^\dagger_k b_k + \sum_k e^{-ik(r^b_i - r^a_i)} b^\dagger_k a_k \\
&+ \sum_k e^{ik(r^a_{i} - r^b_{i-1})} b^\dagger_k a_k + \sum_k e^{-ik(r^a_{i} - r^b_{i-1})} a^\dagger_k b_k]
\end{aligned}\\
&= -t[\sum_k e^{ik(r^a_{i} - r^b_{i-1})}+e^{-ik(r^b_i - r^a_i)}]b^\dagger_k a_k -t[\sum_k e^{ik(r^b_i - r^a_i)}+e^{-ik(r^a_{i} - r^b_{i-1})}]a^\dagger_k b_k \\
&= \sum_k 2\cos(k\Delta) b^\dagger_k a_k + \sum_k 2\cos(k\Delta) a^\dagger_k b_k
\end{aligned}
\tag{10} H ^ = − t i ∑ ( a i † b i + b i † a i + b i − 1 † a i + a i † b i − 1 ) = − N t i ∑ ( k ∑ e − ik r i a a k † k ′ ∑ e ik r i b b k + k ∑ e − ik r i b b k † k ′ ∑ e ik r i a a k + k ∑ e − ik r i − 1 b b k † k ′ ∑ e ik r i a a k + k ∑ e − ik r i a a k † k ′ ∑ e ik r i − 1 b b k ) = − t [ k ∑ e ik ( r i b − r i a ) a k † b k + k ∑ e − ik ( r i b − r i a ) b k † a k + k ∑ e ik ( r i a − r i − 1 b ) b k † a k + k ∑ e − ik ( r i a − r i − 1 b ) a k † b k ] = − t [ k ∑ e ik ( r i a − r i − 1 b ) + e − ik ( r i b − r i a ) ] b k † a k − t [ k ∑ e ik ( r i b − r i a ) + e − ik ( r i a − r i − 1 b ) ] a k † b k = k ∑ 2 cos ( k Δ ) b k † a k + k ∑ 2 cos ( k Δ ) a k † b k ( 10 ) where $\Delta$ is the lattice vector length.
using $b^\dagger_k a_k$ and $a^\dagger_k b_k$ as basis, we can write the Hamiltonian in reciprocal space as:
H = ( 0 − 2 t cos ( k Δ ) − 2 t cos ( k Δ ) 0 ) (11) H = \left( \begin{matrix} 0 & -2t\cos(k\Delta) \\ -2t\cos(k\Delta) & 0 \end{matrix} \right)
\tag{11} H = ( 0 − 2 t cos ( k Δ ) − 2 t cos ( k Δ ) 0 ) ( 11 ) Diagonalize this matrix by means like:
∣ E I − H ∣ = 0 (12) |EI - H | = 0
\tag{12} ∣ E I − H ∣ = 0 ( 12 ) we get the eigenvalues (aka bands):
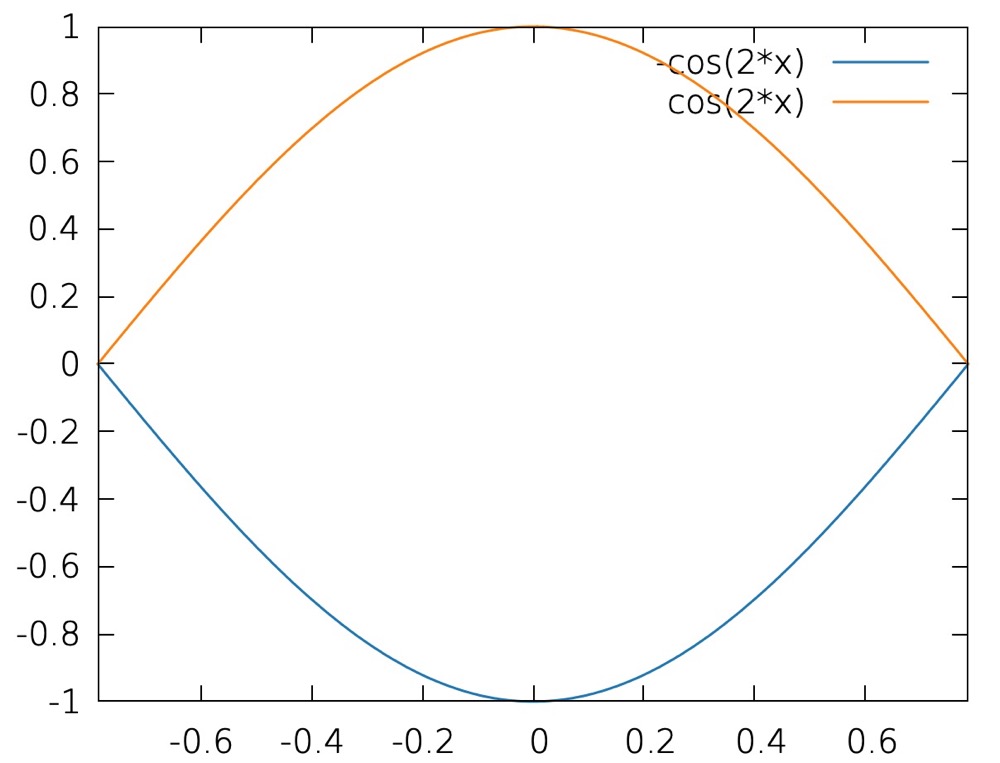
E 1 ( k ) = + 2 t cos ( k Δ ) E 2 ( k ) = − 2 t cos ( k Δ ) (13) \begin{aligned}
E_{1}(k) = + 2t\cos(k\Delta)\\
E_{2}(k) = - 2t\cos(k\Delta)\\
\end{aligned}
\tag{13} E 1 ( k ) = + 2 t cos ( k Δ ) E 2 ( k ) = − 2 t cos ( k Δ ) ( 13 ) which looks like:
we see that the BZ is now halved, this is actually due to band folding. Still, every bit of information is preserved here, for example, at $\Gamma$ point. the upper band corresponds to the states at the edge of the primitive BZ.
The eigenvectors can be obtained by solving the equations:
( E I − H ) A = 0 (EI-H)A = 0 ( E I − H ) A = 0 where $E$ is the dispersion, $I$ is the identity matrix, $A$ is the eigenvectors.
Here the eigenvectors are:
A 1 = 1 2 ( 1 1 ) A 2 = 1 2 ( 1 − 1 ) (14) \begin{aligned}
A_1 = \frac{1}{\sqrt{2}}\left( \begin{matrix} 1 \\ 1 \end{matrix} \right)\\
A_2 = \frac{1}{\sqrt{2}}\left( \begin{matrix} 1 \\ -1 \end{matrix} \right) \\
\end{aligned}
\tag{14} A 1 = 2 1 ( 1 1 ) A 2 = 2 1 ( 1 − 1 ) ( 14 ) again, we can get the real space representation using inverse FT:
A k 1 ( r ) = 1 1 N ∑ j e i k r j a j ( r ) + 1 1 N ∑ j e i k r j b j ( r ) A k 2 ( r ) = 1 1 N ∑ j e i k r j a j ( r ) − 1 1 N ∑ j e i k r j b j ( r ) (15) \begin{aligned}
A^1_{k}(r) &= 1 \frac{1}{\sqrt{N}} \sum_j e^{ikr_j} a_j(r) + 1 \frac{1}{\sqrt{N}} \sum_j e^{ikr_j} b_j(r)\\
A^2_{k}(r) &= 1 \frac{1}{\sqrt{N}} \sum_j e^{ikr_j} a_j(r) - 1 \frac{1}{\sqrt{N}} \sum_j e^{ikr_j} b_j(r)
\end{aligned}
\tag{15} A k 1 ( r ) A k 2 ( r ) = 1 N 1 j ∑ e ik r j a j ( r ) + 1 N 1 j ∑ e ik r j b j ( r ) = 1 N 1 j ∑ e ik r j a j ( r ) − 1 N 1 j ∑ e ik r j b j ( r ) ( 15 ) Flavour 2
In this flavour, we act directly the Bloch wavefunctions on to the Hamiltonian.
Steps to solve real-space TB hamiltonian
write out the expression of the Hamiltonian matrix.
change one of the exponential $e^{ikr}$ to $e^{ik(r-r’)} \cdot e^{ikr’}$.
use the definition of Dirac delta function: $\delta(k,k’) = \frac{1}{N} \sum_j e^{i(k-k’)r_i}$.
do the same thing with all atoms and construct the full Hamiltonian using the elements we got.
First, we have the Fourier relation (discrete FT with respect to the lattice, this is basically an anti-Wannierization process):
ψ k ⃗ α ( r ⃗ ) = 1 N ∑ R α exp ( i k ⃗ R α ) ϕ R α α ( r ⃗ ) (16) \psi^{\alpha}_{\vec k}(\vec r) = \frac{1}{\sqrt{N}} \sum_{R_{\alpha}} \exp(i \vec k R_{\alpha})\phi^{\alpha}_{R_{\alpha}}(\vec r)
\tag{16} ψ k α ( r ) = N 1 R α ∑ exp ( i k R α ) ϕ R α α ( r ) ( 16 ) where $\alpha$ labels the orbital inside one unitcell and the unitcell is labeled by $\vec R_{\alpha}$.
We have $N$ unitcell to consider (summation goes up to $N$), the $\frac{1}{\sqrt{N}}$ is used to normalization the result.
In reverse (we are not going to use this relation in this note but just for the sake of completeness):
ϕ R α α ( r ⃗ ) = 1 N ∑ k ⃗ exp ( − i k ⃗ R ⃗ α ) ψ k ⃗ α ( r ⃗ ) (17) \phi^{\alpha}_{R_{\alpha}}(\vec r) = \frac{1}{\sqrt{N}} \sum_{\vec k} \exp(-i \vec k \vec R_{\alpha})\psi^{\alpha}_{\vec k}(\vec r)
\tag{17} ϕ R α α ( r ) = N 1 k ∑ exp ( − i k R α ) ψ k α ( r ) ( 17 ) Now, the Hamiltonian elements (in reciprocal space) can be calculated by sandwiching it in between two Bloch functions. i.e.:
H α β = ⟨ ψ k ⃗ α ( r ⃗ ) ∣ H ^ ∣ ψ k ⃗ β ( r ⃗ ) ⟩ (18) H_{\alpha \beta} = \bra{\psi^{\alpha}_{\vec k}(\vec r)} \hat H \ket{\psi^{\beta}_{\vec k}(\vec r)}
\tag{18} H α β = ⟨ ψ k α ( r ) ∣ H ^ ∣ ψ k β ( r ) ⟩ ( 18 ) Note that the Hamiltonian ($\hat H$) here is still expressed as:
H = − 1 2 ∇ 2 + V ( r ) (19) H = -\frac{1}{2} \nabla^2 + V(r)
\tag{19} H = − 2 1 ∇ 2 + V ( r ) ( 19 ) Now, if we plug in Eq. 1 to Eq. 3, we get:
H α , β = ∑ k ⃗ , k ⃗ ′ ⟨ ψ k ⃗ α ( r ⃗ ) ∣ H ^ ∣ ψ k ⃗ ′ β ( r ⃗ ) ⟩ = 1 N ∑ k ⃗ , k ⃗ ′ ∑ R ⃗ α exp ( − i k ⃗ R ⃗ α ) ⟨ ϕ R ⃗ α α ( r ⃗ ) ∣ H ^ ∑ R ⃗ β exp ( i k ⃗ ′ R ⃗ β ) ∣ ϕ R ⃗ β β ( r ⃗ ) ⟩ = ∑ k ⃗ , k ⃗ ′ ∑ R ⃗ α 1 N exp ( i R ⃗ α [ k ⃗ ′ − k ⃗ ] ) ∑ R ⃗ β exp ( i k ⃗ ′ [ R ⃗ β − R ⃗ α ] ) ⟨ ϕ R ⃗ α α ( r ⃗ ) ∣ H ^ ∣ ϕ R ⃗ β β ( r ⃗ ) ⟩ = ∑ k ⃗ , k ⃗ ′ δ ( k ⃗ ′ − k ⃗ ) ∑ R ⃗ β exp ( i k ⃗ ′ [ R ⃗ β − R ⃗ 0 ] ) ⟨ ϕ R ⃗ 0 α ( r ⃗ ) ∣ H ^ ∣ ϕ R ⃗ β β ( r ⃗ ) ⟩ = ∑ R ⃗ β exp ( i k ⃗ [ R ⃗ 0 − R ⃗ β ] ) ⟨ ϕ R ⃗ 0 α ( r ⃗ ) ∣ H ^ ∣ ϕ R ⃗ β β ( r ⃗ ) ⟩ = ∑ R ⃗ β exp ( i k ⃗ [ R ⃗ 0 − R ⃗ β ] ) ⋅ ( − t α , β R ⃗ 0 , R ⃗ β ) = H α , β ( k ⃗ ) (20) \begin{align}
H_{\alpha,\beta} &= \sum_{\vec k, \vec k'} \bra{\psi^{\alpha}_{\vec k}(\vec r)} \hat H \ket{\psi^{\beta}_{\vec k'}(\vec r)}\\
&=\frac{1}{N} \sum_{\vec k, \vec k'} \sum_{\vec R_{\alpha}} \exp(-i \vec k \vec R_{\alpha}) \bra{\phi^{\alpha}_{\vec R_{\alpha}}(\vec r)} \hat H \sum_{\vec R_{\beta}} \exp(i \vec k' \vec R_{\beta}) \ket{\phi^{\beta}_{\vec R_{\beta}}(\vec r)} \\
&=\sum_{\vec k, \vec k'} \sum_{\vec R_{\alpha}} \frac{1}{N} \exp(i\vec R_{\alpha} [\vec k' - \vec k]) \sum_{\vec R_{\beta}} \exp(i \vec k' [\vec R_{\beta}-\vec R_{\alpha}]) \bra{\phi^{\alpha}_{\vec R_{\alpha}}(\vec r)} \hat H \ket{\phi^{\beta}_{\vec R_{\beta}}(\vec r)} \\
&= \sum_{\vec k, \vec k'} \delta(\vec k' - \vec k) \sum_{\vec R_{\beta}} \exp(i \vec k' [\vec R_{\beta}-\vec R_{0}]) \bra{\phi^{\alpha}_{\vec R_{0}}(\vec r)} \hat H \ket{\phi^{\beta}_{\vec R_{\beta}}(\vec r)} \\
&= \sum_{\vec R_{\beta}} \exp(i \vec k [\vec R_{0}- \vec R_{\beta}]) \bra{\phi^{\alpha}_{\vec R_{0}}(\vec r)} \hat H \ket{\phi^{\beta}_{\vec R_{\beta}}(\vec r)} \\
&= \sum_{\vec R_{\beta}} \exp(i \vec k [\vec R_{0}- \vec R_{\beta}]) \cdot (-t^{\vec R_{0},\vec R_{\beta}}_{\alpha, \beta}) = H_{\alpha, \beta}(\vec k)
\end{align}
\tag{20} H α , β = k , k ′ ∑ ⟨ ψ k α ( r ) ∣ H ^ ∣ ψ k ′ β ( r ) ⟩ = N 1 k , k ′ ∑ R α ∑ exp ( − i k R α ) ⟨ ϕ R α α ( r ) ∣ H ^ R β ∑ exp ( i k ′ R β ) ∣ ϕ R β β ( r ) ⟩ = k , k ′ ∑ R α ∑ N 1 exp ( i R α [ k ′ − k ]) R β ∑ exp ( i k ′ [ R β − R α ]) ⟨ ϕ R α α ( r ) ∣ H ^ ∣ ϕ R β β ( r ) ⟩ = k , k ′ ∑ δ ( k ′ − k ) R β ∑ exp ( i k ′ [ R β − R 0 ]) ⟨ ϕ R 0 α ( r ) ∣ H ^ ∣ ϕ R β β ( r ) ⟩ = R β ∑ exp ( i k [ R 0 − R β ]) ⟨ ϕ R 0 α ( r ) ∣ H ^ ∣ ϕ R β β ( r ) ⟩ = R β ∑ exp ( i k [ R 0 − R β ]) ⋅ ( − t α , β R 0 , R β ) = H α , β ( k ) ( 20 ) here, we’ve taken advantage of the fact that we are summing over a huge amount of real-space cells ($\vec R_{\alpha}$ and $\vec R_{\beta}$),
∑ R ⃗ β exp ( i k ⃗ ′ [ R ⃗ β − R ⃗ α ] ) ⟨ ϕ R ⃗ α α ( r ⃗ ) ∣ H ^ ∣ ϕ R ⃗ β β ( r ⃗ ) ⟩ \sum_{\vec R_{\beta}} \exp(i \vec k' [\vec R_{\beta}-\vec R_{\alpha}]) \bra{\phi^{\alpha}_{\vec R_{\alpha}}(\vec r)} \hat H \ket{\phi^{\beta}_{\vec R_{\beta}}(\vec r)} R β ∑ exp ( i k ′ [ R β − R α ]) ⟨ ϕ R α α ( r ) ∣ H ^ ∣ ϕ R β β ( r ) ⟩ can be replaced with:
∑ R ⃗ β exp ( i k ⃗ ′ [ R ⃗ β − R ⃗ 0 ] ) ⟨ ϕ R ⃗ 0 α ( r ⃗ ) ∣ H ^ ∣ ϕ R ⃗ β β ( r ⃗ ) ⟩ . \sum_{\vec R_{\beta}} \exp(i \vec k' [\vec R_{\beta}-\vec R_{0}]) \bra{\phi^{\alpha}_{\vec R_{0}}(\vec r)} \hat H \ket{\phi^{\beta}_{\vec R_{\beta}}(\vec r)}. R β ∑ exp ( i k ′ [ R β − R 0 ]) ⟨ ϕ R 0 α ( r ) ∣ H ^ ∣ ϕ R β β ( r ) ⟩ . In the last step, since the Hamiltonian is still in real space, we can calculate the integral directly in real space and the resulting energy ($-t^{\vec R_{0},\vec R_{\beta}}_{\alpha, \beta}$) is the so-called hopping energy.
If $\alpha = \beta$ and $\vec R_{0} = \vec R_{\beta}$, then we call this hopping the “On-site” hopping (energy).
Also note that for the “on-site” energy term, since $\alpha = \beta$ and $\vec R_{0} = \vec R_{\beta}$, $H_{\alpha, \beta}$ does not depend on the wave vector $\vec k$.
Now that we have the Hamiltonian elements in reciprocal space, all we need to do to get the band structure is to set a $\vec k$ and diagonalize the Hamiltonian.
Important take-away
The Hamiltonian in the rec space can be simply constructed using the following relation:
H α , β ( k ⃗ ) = ∑ R ⃗ β exp ( i k ⃗ [ R ⃗ 0 − R ⃗ β ] ) ⋅ ( − t α , β R ⃗ 0 , R ⃗ β ) (21) H_{\alpha,\beta} (\vec k) = \sum_{\vec R_{\beta}} \exp(i \vec k [\vec R_{0}- \vec R_{\beta}]) \cdot (-t^{\vec R_{0},\vec R_{\beta}}_{\alpha, \beta})
\tag{21} H α , β ( k ) = R β ∑ exp ( i k [ R 0 − R β ]) ⋅ ( − t α , β R 0 , R β ) ( 21 ) and all we need is the real-space hopping amplitude which can be easily obtained from wannier90_hr.dat.
😉 keep a note of this relation for we’ll need it for next post’s surface green function calculations!
![]() this for introduction to TB method in a QFT perspective.
this for introduction to TB method in a QFT perspective.![]() this for introduction to TB method in a solid state physics perspective.
this for introduction to TB method in a solid state physics perspective.