Some thoughts on periodicity and charge understanding of the polarization Quantum

Heuristic definition of polarization

Electrical polarization, defined as “dipole moments per unit volume”, can heuristically calculated by: \(\textbf{P}_{cell} = \frac{1}{V_{cell}} \int_{cell} d\textbf{r} \textbf{r} \rho(\textbf{r}),\) where the integration is carried out over one unit cell. Note that for DFT results, this formula only applies to electron density and the point charge ionic contribution can be later on added.

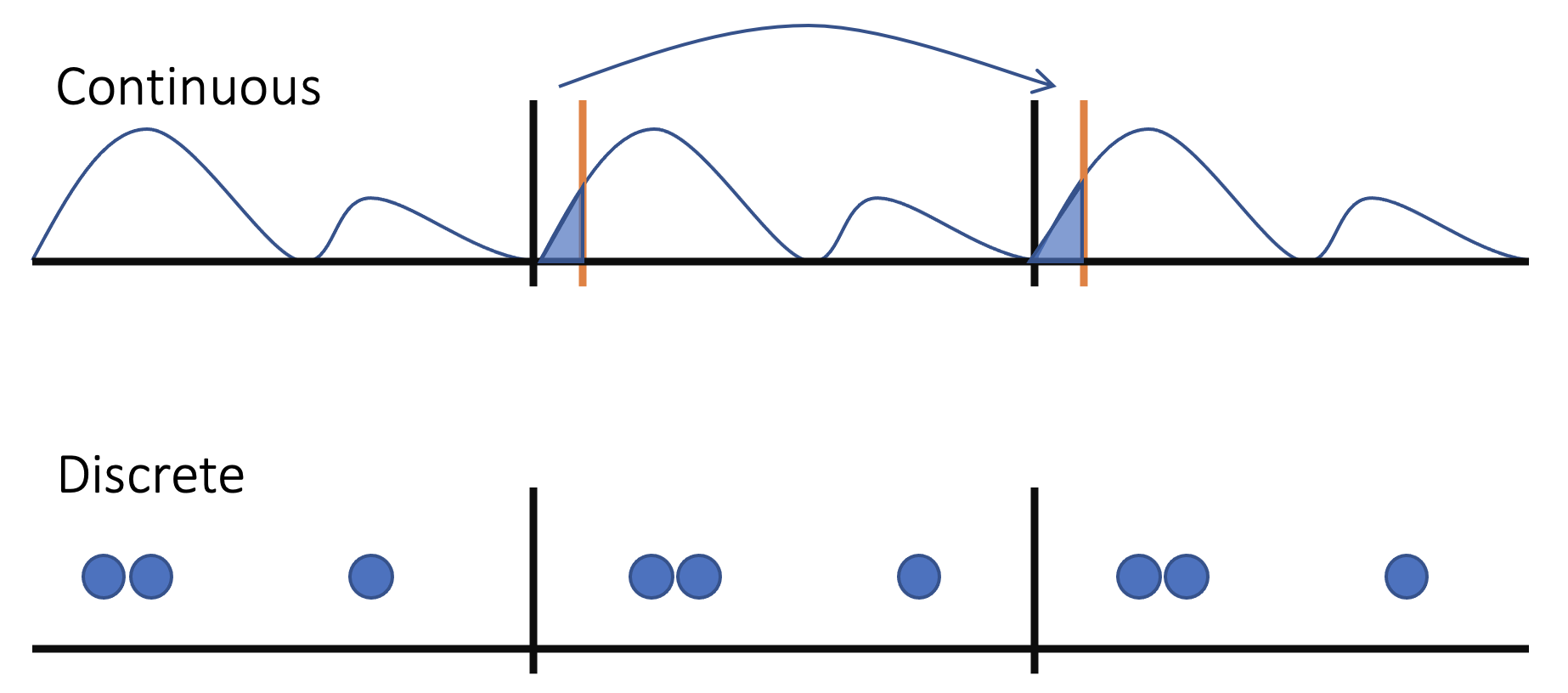
As shown on the top panel, one can see that if the we can somehow treat the charge density as a point-like charge distribution, the integration can be discretized into summation:

\[\textbf{P}_{cell} = \sum_{i=0}^{N} \textbf{r}_i Q_{i},\]

where i labels each electron and \(\textbf{r}_i\), \(Q_i\) stands for the location and charge of electron \(i\). Note that not only this formula is more chemically intuitive and calculation-friendly, it tells us that as long as the point charge does not cross the border of the unit cell (we’ll talk about when it does later), we can randomly move the definition of the cell without changing the polarization value.

However, real materials are not that easy to deal with (they rarely are, which is the reason why we find them fascinating!). The charge distribution for real materials is continuous and the integration is continuously depends on the location of the cell. For example, if we move the cell to right a little bit, we are essentially transporting part of our charge from the left hand side of our cell to the right hand side, and that, my friend, means our polarization also changes.

The question is, how much does it actually change?

Translation effect to the polarization

To show the effect of cell translation the polarization, let’s consider a one-dimensional periodical charge density \(\rho\). For shit charge density distribution, we can write the polarization as:

\[P_{x} = \int_{-a/2}^{a/2} x \rho(x) dx,\]

where a is the cell length. If we transform our cell to the left by a length of \(x_i\), we can write the polarization again as:

\[\begin{align} P_{x'} &= \int_{-a/2}^{a/2} (x+x_i) \rho(x+x_i) dx \end{align}\]

and we can do some algebra on it:

\[\begin{align} P_{x'} &= \int_{-a/2}^{a/2} (x+x_i) \rho(x+x_i) dx \\ &= \int_{-a/2}^{a/2} x \rho(x+x_i) dx + x_i \int_{-a/2}^{a/2} \rho(x+x_i) dx \\ &= \int_{-a/2+x_i}^{a/2+x_i} (C+x_i) \rho(C) dC + x_i \int_{-a/2}^{a/2} \rho(x+x_i) dx \\ &= \int_{-a/2+x_i}^{a/2+x_i} (C) \rho(C) dC - x_i \int_{-a/2+x_i}^{a/2+x_i} \rho(C) dC + x_i \int_{-a/2}^{a/2} \rho(x+x_i) dx, \end{align}\]

here, we have substituted \(x+x_i\) with \(C\). Because the integration of \(\rho(x)\) over one cell length always equals to the number charge of one cell, the later two terms cancel each other and leave us:

\[\begin{align} P_{x'} &= \int_{-a/2+x_i}^{a/2+x_i} (C) \rho(C) dC \\ &= \int_{-a/2+x_i}^{a/2} (C) \rho(C) dC + \int_{a/2}^{a/2+x_i} (C) \rho(C) dC \\ &= \int_{-a/2+x_i}^{a/2} (C) \rho(C) dC + \int_{0}^{x_i} (C+\frac{a}{2}) \rho(C+\frac{a}{2}) dC \end{align}\]

Using periodicity of the charge density:

\[\begin{align} P_{x'} &= \int_{-a/2+x_i}^{a/2} (C) \rho(C) dC + \int_{0}^{x_i} (C+\frac{a}{2}) \rho(C+\frac{a}{2}) dC \\ &= \int_{-a/2+x_i}^{a/2} (C) \rho(C) dC + \int_{0}^{x_i} (C+\frac{a}{2}) \rho(C-\frac{a}{2}) dC \\ &= \int_{-a/2+x_i}^{a/2} (C) \rho(C) dC + \int_{0}^{x_i} (C-\frac{a}{2}+a) \rho(C-\frac{a}{2}) dC \\ &= \int_{-a/2+x_i}^{a/2} (C) \rho(C) dC + \int_{0}^{x_i} (B+a) \rho(B) dB \\ &= \int_{-a/2+x_i}^{a/2} (C) \rho(C) dC + \int_{-a/2}^{-a/2+x_i} (B) \rho(B) dB + a \int_{-a/2}^{-a/2+x_i} \rho(B) dB \\ &= \int_{-a/2}^{a/2+} (C) \rho(C) dC + a \int_{-a/2}^{-a/2+x_i} \rho(B) dB \end{align}\]

Okay, now let analyze what we’ve got here: the first term equals to the original polarization where we never touched the definition of our cell, and the second term is the charge that jumps from one left part of the cell to the right side dotted by lattice length which is the length they jumped.

Compare to the polarization quantum

Now what does this translate to the polarization quantum in the modern theory of polarization? Remember our discretized version of the polarization? If we also discretize our result, we get:

\[\begin{align} P_{x'} &= \int_{-a/2}^{a/2} (C) \rho(C) dC + a \int_{-a/2}^{-a/2+x_i} \rho(B) dB \\ P_{x'} &= \sum_{i=0}^{N} \textbf{r}_i Q_{i} + a \sum_{i=x} Q_{i}, \end{align}\]

where x stands for the labels of those electron centers that crossed the border of our cell. (Assuming x_i is large enough that some Wannier centers crossed the border) The second term in this equation is the so-called polarization quantum.

That’s it! Enjoy your ho-ho-holidays eveyone!!! 🎄