Is it really necessary to have a centrosymmetric structure to calculate the macroscopic polarization?

Background

According to “the Modern theory of polarization”, in a continous-k formulation, the polarization of one structure \(\mathbf{P}_{el}\) is \(- f e / (2 \pi)^3\) times the sum of valence-band’s Berryphase while the total macroscopic polarization is the polairzation difference between ferroelectric phase and the centrosymmetric phase. Convieniently, Wannier charge centers can be linked to the Berryphase of valence band via a Fourier transformation. Thus, we should be able to calculate the ferroelectric polarization using Wannier centers to be more chemically intuitive.

In definition, this calculation seems to be easily achievable, but in pratice, there are many pitfalls in doing such calculations. However, almost all of these pitfalls or problems are due to the so called polairzation quantum which arise from the periodicity of the unitcell (Translation symmetry of crystals). My previous post already demonstrated how easy can one fall in to such trap and get erroneous results and, in essence, this post is still deeply linked with such problems.

Big questions

What is the “correct” way of making the centrosymmetric phase in order to get the correct polarization value?

NEB calculation to determine the optimum transition structure?
Linear transform from one polarized state to another?

What if there are multiple high-symmetry phases, which one do we choose???

Since the actual structural change during the polarization shift will almost always not be uniform, how can our result match the one experiementalist get??

TL;DR

__It doesn’t matter which centrosymmetric structure one use, as long as we have a smooth transformation, every centrosymmetric phase will have the same polarization value. Correspondingly, their Berrypahse will always be the same if we are able to avoid band crossing

Also, yes, band crossing does mess up the result. But if we are careful enough to keep track of the continuous band transformation and able to disentangle (eliminate) the effect of the band crossing, we can still get the right answer.__

Study case

I’ll try to explain this with a simple BTO structure. Here, different from the last time, I’ve constrained my structure to only allow Ti atom to move:

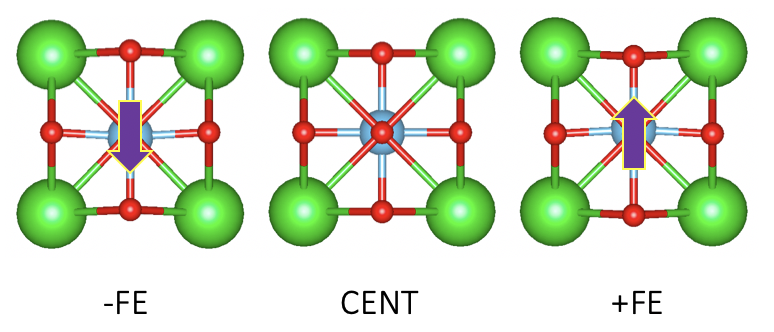
The result:

Total ionic contribution = -0.6907 elect*A
Total electronic contribution = 0.27726 elect*A
Total dipole moment = -0.41344 elect*A
Volume = 64.35864801 A^3

Total polarization = 0.102912491 C/m^2

What if, I construct an simple antiferroelectric structure and say that is the centrosymmetric phase I take as referencing structure?

Recall there are acatually no more constraints other than our reference structure to be centrosymmetric, so, this actually does not contradict any rules.

The result:

Total ionic contribution = -1.38139 elect*A
Total electronic contribution = 0.55453 elect*A
Total dipole moment = -0.82686 elect*A
Volume = 128.717296 A^3

Total polarization = 0.102912491 C/m^2

Interestingly, using AFE structure as the reference phase, I got identical polarization value comparing to the usual cubic phase.

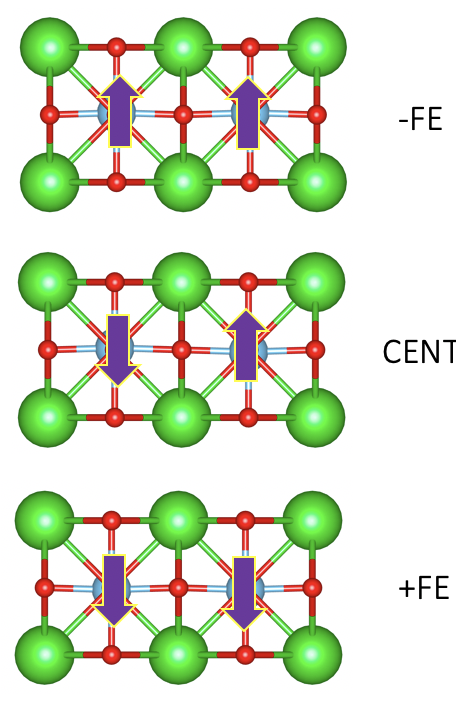
Let’s slow down and think about why this is the case. In oue switching route, we can clearly see that from FE to AFE structrue, the Ti atom on the left hand side needs to go down around 0.115A. On the other hand, if we have a supercell with both Ti atoms at the center of their cell, each Ti only needs to go down 0.057A, exactly half of the length in the AFE case. This tells us, in our AFE case, we have one Ti atom doing all the hard work while the other doing nothing. This does not change the fact that eventually all the work done for the polarization switching will always be there.

Now, Lets go one step further…

Here, we can actually see this giant AFE structure as two FE grain with one boundary sandwiched in between. Similar to our two-cell AFE case, this can still be used to calculate the total polarization. This tells us that we can even construct a centrosymmetric macroscopic structrue with grain boundary in it. As long as it has centrosymmetry and can be smoothly transformed form the positive FE phase to the negative FE phase, our reulst will always remains the same!

This actually reassures us the polarization does not depend on the centrosymmetric phase and only depend on the ferroelectric phase like a lone dipole moment without translation symmetry (as it should be). The symmetry protecting the berry phase of the centrosymmetric structure is the inversion symmetry (or in some case mirror symmetry).

Summary

In summary, the centrosymmetric phase in the calculation of macroscopic polarization actually does not matter that much. As long as you can keep track of the band structure and the polarization vs distortion curve to be on the same branch, you are safe.

Or, if you are savy enough, you can use Wannier90’s disentanglement to solve the “metallic centrosymmetric phase” problem.

Input

I’ve put all input file in a zip file for download: VASP. I’ve also included a 2D inplane ferroelectric structure with two usable centrosymmetric phases to play with. enjoy!