Searching for a shell
Testing Berry phase method in VASP and QE for 2D system
The VASP and QE both have berry phase module that calculate the electronic polarization “automagically”. However, their results always seem to be puzzling, especially for low dimensional systems. In order to get a clear picture of how to these routines perform for 2D systems and to show how to use them correctly, a 2D ferroelectric $\mathrm{NbN}$ system is employed as an example. To confirm their results, a charge-center method was also employed. As a comparison, a 3D prototypical ferroelectric $\mathrm{BaTiO_3}$ system is also studied here.
Before diving into things, let’s review some basic concepts so that we can be sure that we know what we are about to do.
Background
According to the modern theory of polarization, the electrical polarization depends on the difference of dipole moment between centrosymmetric structure and non-centrosymmetric structure. The reason behind is that the polarization cannot be uniquely determined due to periodical boundary conditions.(That is, translation of unit cell vector can yield unphysical movements in the charge centers.)
To illustrate this, first, let’s consider an imaginary one dimensional atomic chain that have two different atoms: an anion and a cation.

We can easily determine the dipole moment pointing from the anion to the cation.
However, the physical world does not work in such simple way. If we take a step further, differentiate the electrons and ions, the problem becomes much harder to solve:
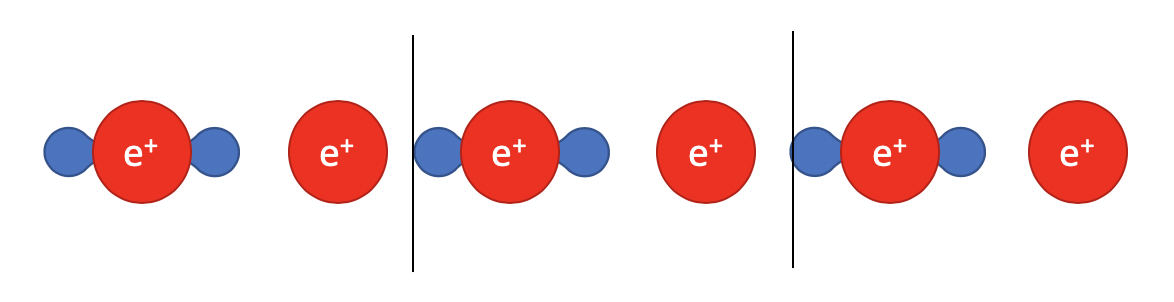
Here, the electrons are represented as charge density and are spread out between two ions. To get the charge center for electrons, we have to integrate the charge density in the unit cell:
And the positive charge center can be found:
These expressions are easy to solve, but the charge-center varies with the choice of unicell. For example, if we translate the unitcell by a fraction to the right:
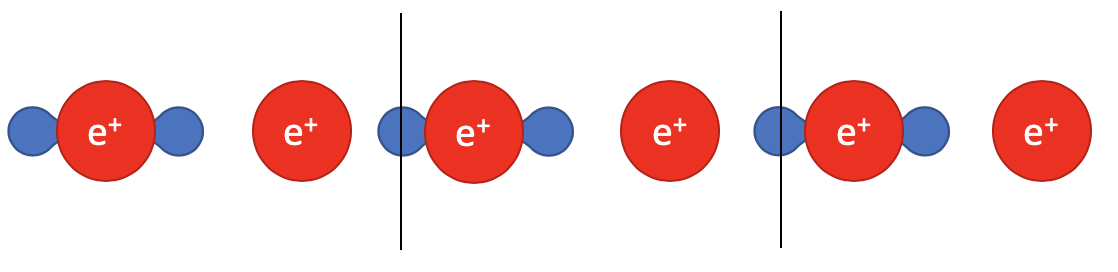
Taking a closer look at the charge distribution, some of which “jumped” from the left end to the right end due to periodical conditions. And even though the structure is unchanged, this translation motion changes the charge center of electrons while left the ion center unaffected.
To eliminate this ambiguity, Vanderbilt and others found out that it is not the dipole moment for non-centrosymmetric phase that matters, the actual polarization depends on the change of polarization from the non-centrosymmetric phase to the centrosymmetric phase.
Side Note: how to define a centrosymmetric phase?
Answer: Calculate optimum transition route and extract the local maxima as centrosymmetric phase.
VASP 2D System
2D-$\mathrm{NbN}$, as an out of plane ferroelectric system suggested by Anuja et al, have exotic switchable out-of-plane (OOP) polarization which can happen without switching of ionic positions. I choose this to show how Berry phase method can, sometimes, be cumbersome and have boundaries in certain systems.
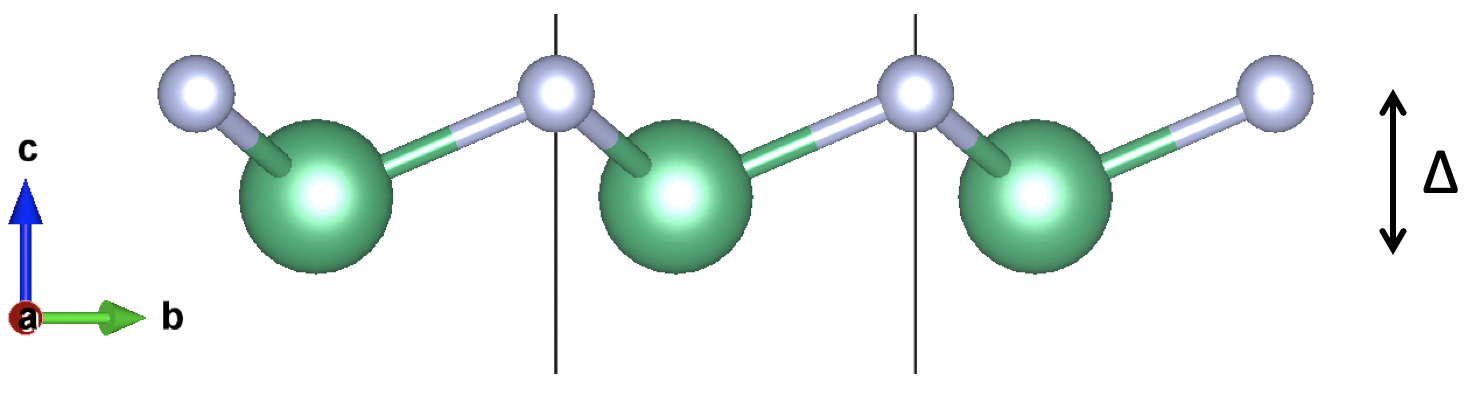
The system consist of one Nb and one N atom that forms a Boron Nitride like structure. The polarization can be switched by switching the in the z axis:
Due to the fact that this structure possess OOP polarization in which the periodical conditions are broken, the charge center can be uniquely defined since the charge density reverts to zero at the vacuum region.
The vacuum region is chosen as around 30 Angstrom with an atrifical dipole layer so that imaging counterpart has no effects.
Charge center method
The charge center method is performed using this tool (![]() link). The final polarization obtained for intrinsic $\mathrm{NbN}$ monolayer is:
link). The final polarization obtained for intrinsic $\mathrm{NbN}$ monolayer is:
And the transition curve is obtained almost identical to the published result:
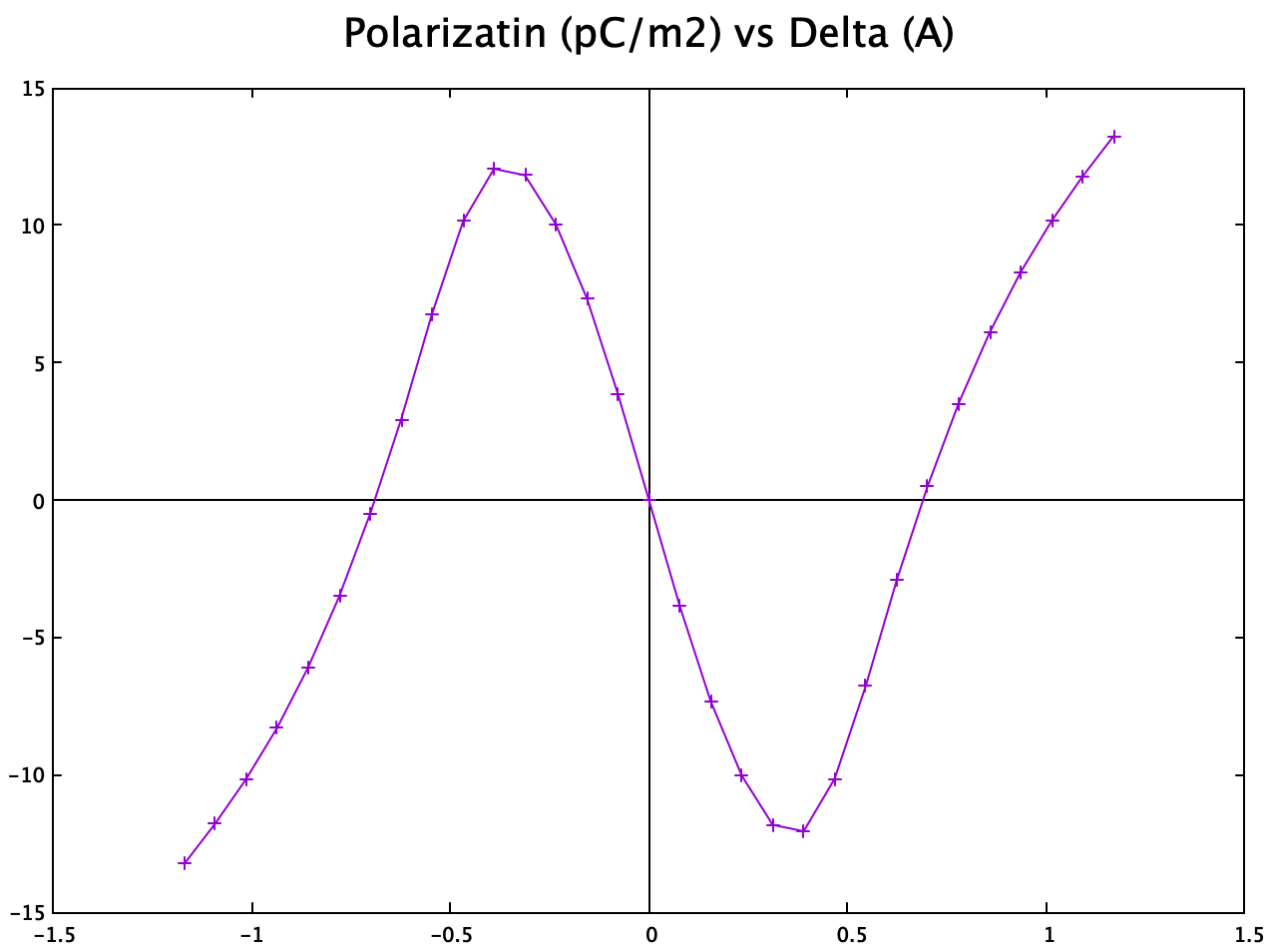
This confirms the correctness of my charge center method even though in paper they used the Berryphase method.
Berryphase method
To avoid potential pitfalls as mentioned in ![]() link, I performed both automatic and manual Berryphase calculation using the tag:
link, I performed both automatic and manual Berryphase calculation using the tag:
LDIPOL = .TRUE.
IDIPOL = 3
DIPOL = 0.5 0.5 0.2681174992499997
LCALCPOL = .T.
and
LDIPOL = .TRUE.
IDIPOL = 3
DIPOL = 0.5 0.5 0.26378659
LBERRY = .TRUE.
IGPAR = 3
NPPSTR = 1
The final results does not make sense as:
Ionic dipole moment: p[ion]=( -10.24777 5.91655 0.00000 ) electrons Angst
Total electronic dipole moment: p[elc]=( -3.63403 2.09811 29.94773 ) electrons Angst
and
e<r>_ev=( 0.00209 0.00028 -0.01672 ) e*Angst
e<r>_bp=( 0.00000 0.00000 29.96212 ) e*Angst
Total electronic dipole moment: p[elc]=( 0.00209 0.00028 29.94540 ) e*Angst
ionic dipole moment: p[ion]=( -6.30632 12.74335 0.00000 ) e*Angst
No matter how I tried: a different k-point set, a different DIPOL value … the p[elc] does not change and stays at around $30$ e*Angst.
One thing that I notice: changing DIPOL tag greatly affects the convergence (potentially due to added dipole corrections not being inside the vacuum layer) and the value of p[ion]. But it does absolutely nothing to p[elc].
As it turns out, setting NPPSTR=1 is problematic as the Berryphase calculation needs to calculate the phase difference between at least two wavefunctions. This question has also been disscussed on ![]() this post on VASP forum.
this post on VASP forum.
So, what about periodical directions?
VASP 3D system
Berryphase
Now lets consider prototypical system:
By varying the atomic displacement from the centrosymmetric phase (CENT) to ferroelectric one (FE). VASP produce a series of ionic and electronic contribution to the total dipole moment.
| Image | Ion (elect*A) | Electron (elect*A) |
|---|---|---|
| 0 (CENT) | +00.00000 | +0.00000 |
| 1 | -12.01278 | -0.29138 |
| 2 | -11.92507 | -0.58047 |
| 3 | -11.83735 | -0.86532 |
| 4 | -11.74963 | -1.14461 |
| 5 | -11.66192 | -1.41757 |
| 6 (FE) | -11.5742 | -1.68399 |
It is clear that the centrosymmetric one has a wrong ionic contribution to the total polarziation.
At first, I thought this is due to the imposed symmetry constraint. However, after switch off symmetry entirely (ISYM=-1), VASP still produce this abnormal value of 0.0 elect*A for centrosymmetric phase.
As it turns out, this is actually a bug in VASP, see this post. It should’ve been fixed in VASP v6.3.0.
After figure out which value is clearly wrong, we can now proceed to calculate total polarization by extrapolating the value of p[ion] at centrosymmetric phase and calculate the final polarization as:
Total ionic contribution = 0.5258 elect*A
Total electronic contribution = -1.68399 elect*A
Total dipole moment = -1.15819 elect*A
Volume = 64.35864801 A^3
Total polarization = 0.288293871 C/m^2
Note we have to account for the negative sign of electron for the final value.
This value matches exactly with the one from ![]() this tutorial from Quantumwise and is similar to
this tutorial from Quantumwise and is similar to ![]() the experimental value of 0.26 C/m^2.
the experimental value of 0.26 C/m^2.
By far, every thing works fine for the periodical system in VASP. The only problem is that the centrosymmetric phase’s ionic part cannot be automatically calculated.
There are two way of solving this:
-
Calculate a series of structure points, linear fitting to make sure the polarization is at the same branch.
-
Manually calculate ionic contribution by:
where is the valence electron number of atom $j$ and is its positions (relative to DIPOL). And subtract the centrosymmetric one from the ferroelectric one. The minus sign is to count for the charge sign of electron so that the final ionic contribution is in elect * A.
WARNING The sign convention for the ionic part is very important. If you decided to do the ionic part yourself, remember to add a minus sign to the dipole moments of each structure, and ADD it to VASP’s electronic part (so that they are both in elect * Å). And remember to flip the sign again interms of the final result so that the sign is agin correctly expressed in C/M^2.
So far so good. I am now confident that, at least, VASP’s Berryphase routine works correctly on periodical directions.
QE 2D system
Berryphase
QE uses three tag for Berryphase calculations:
lberry = .true. #switch on berryphase routine
gdir = 3 #z axis
nppstr = 7 #number of kpoint
For 2D system, again, if I choose to use nppstr=1, some error pops up. Changing nppstr to a larger number gives out correct answer.
QE 3D system
QE’s example04 strangely did not calculate the polarization of the centrosymmetric phase.
Here, using prototypical as an example, the total polarization is calculated as:
centrosymmetric phase
VALUES OF POLARIZATION
~~~~~~~~~~~~~~~~~~~~~~
The calculation of phases done along the direction of vector 3
of the reciprocal lattice gives the following contribution to
the polarization vector (in different units, and being Omega
the volume of the unit cell):
P = 0.3069997 (mod 15.2444207) (e/Omega).bohr
P = 0.0007069 (mod 0.0351000) e/bohr^2
P = 0.0404125 (mod 2.0067288) C/m^2
The polarization direction is: ( 0.00000 , 0.00000 , 1.00000 )
Ferroelectric phase
VALUES OF POLARIZATION
~~~~~~~~~~~~~~~~~~~~~~
The calculation of phases done along the direction of vector 3
of the reciprocal lattice gives the following contribution to
the polarization vector (in different units, and being Omega
the volume of the unit cell):
P = 2.4138432 (mod 15.2444207) (e/Omega).bohr
P = 0.0055578 (mod 0.0351000) e/bohr^2
P = 0.3177509 (mod 2.0067288) C/m^2
The polarization direction is: ( 0.00000 , 0.00000 , 1.00000 )
Total polairzation = 0.3177509-0.0404125 = 0.277 C/m2
Almost identical to VASP’s and the experimental value.
Result: QE can be used to calculate total polarization on both periodical and non-periodical directions.
UPDATE-2020-04-01
- The position of the dipole layer in VASP is set by (
DIPOL+0.5) in fractional coordinates. -
LVTOTandLVHARshould converge in vacuum.LVTOTconverges slower thanLVHAR.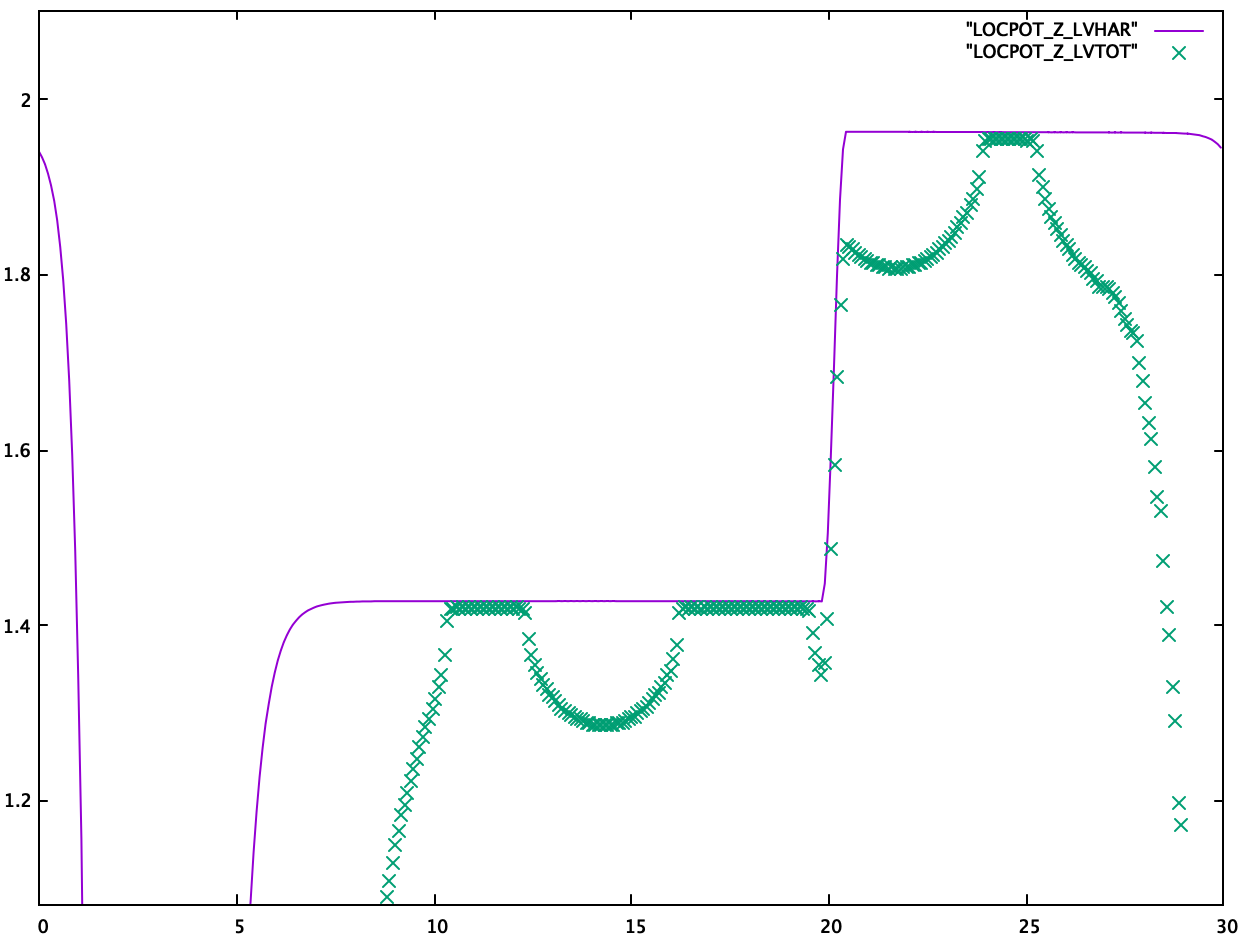
Input
I’ve put all input file in a zip file for download: Excel data,VASP, QE.