Puzzling effects of saw-tooth electric field in DFT code

Background

In VASP wiki:

It is possible to apply an external electrostatic field in slab, or molecular calculations. Presently only a single value can be supplied and the field is applied in the direction selected by IDIPOL=1-3. The electric force field is supplied in units of eV/Å. Dipole corrections to the potential (LDIPOL=.TRUE.) can and should be turned on to avoid interactions between the periodically repeated images.

So the proper procedure to add electric field to a slab or molecular is adding:

EFIELD = 0.2            # Field strength
LDIPOL = .TRUE.         # Add dipole correction
IDIPOL = 3              # Electric field direction
DIPOL  = 0.5 0.5 0.5    # dipole origin

Caveats:

The symmetry should be switched off if the system is centro-symmetric (or at least mirror symmetric in the electric field direction)
DIPOL should be set to the weight center of the structure. After countless tests, it seems this setting is most likely to help with the convergence during electronic minimization.
EFIELD describes the force acted on electrons so it points to the opposite direction of the derivative of the elecostatic potential (data stored in LOCPOT). It’s the opposite of the direction of the commonly defined “electric field” (the direction of the force a positive charge feels. i.e. pointing from a positive charge towards an negative charge).

Result

Using these tags and a 2D graphene layer (made into orthorhombic), I calculated the ion-clamped electric field response focusing on the charge and dipole properties.

The electric field effect can be clearly seen from the integrated local potential profile. Note that the potential shift from higher at the bottom of the cell to lower at the top of the cell, vice versa.

Notice the slope of the local potential in the vacuum region equals to the field strength EFIELD. Here I excluded the exchange part and only included the Hartree part of the local potential.

The dipole moment induced by the potential shift can be seen from the differential charge calculated by:

\rho_\text{diff}=\rho_\text{without field}-\rho_\text{with field}

The result are show below:

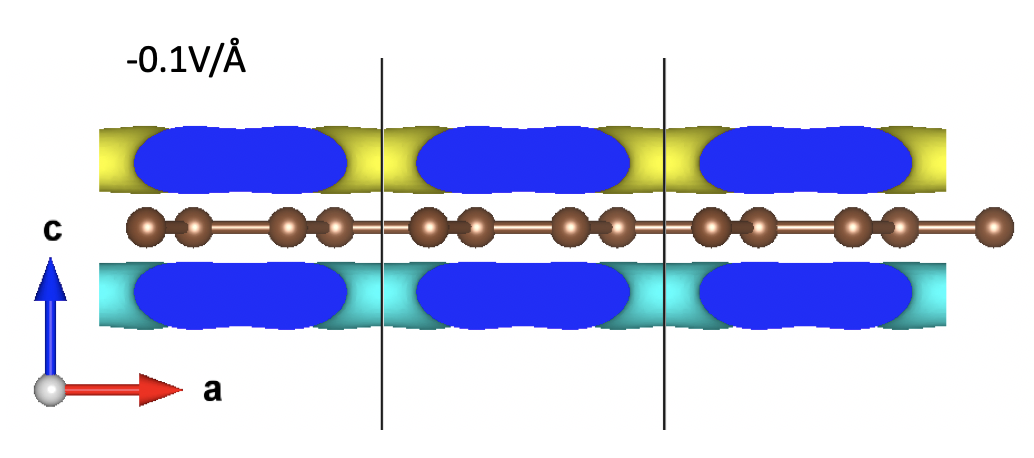
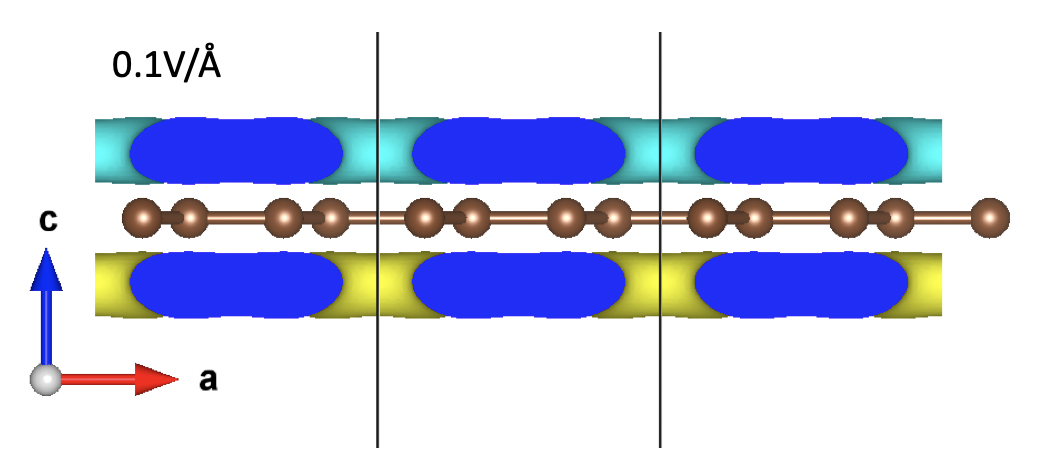
The yellow region indicates charge accumulation while the blue part suggests charge depletion.

Clearly, the “up-ward” electric field (an negative EFIELD) induces electrons to accumulate at the lower region and hence creates an “up-ward” dipole moment (the direction of the dipole moment is defined as pointing from negative charge towards positive charge). Similarly, a “down-ward” electric field (a positive EFIELD) induces a “down-ward” dipole moment.

Problem

The total energy drops with respect to the field strength (in both direction). Since electric field is an external perturbation, this result is unphysical.

In this post, the “admin” of the VASP forum suggest that:

the energy is correct and the first derivative of the energy w.r.t. a field should be the dipole.

Which seems to be faulty since the direction of the dipole moment calculated this way are opposite to the actual one in my calculation.

The energy difference are listed below:

Electric field $\mathscr{E}_\text{field}=0.0/\text{Å}$:

DIPCOR: dipole corrections for dipol
direction  3 min pos     1,
dipolmoment           0.000000      0.000000     -0.000000 electrons x Angstroem
Tr[quadrupol]       -30.699335

energy correction for charged system         0.000000 eV
dipol+quadrupol energy correction           -0.000000 eV
added-field ion interaction          0.000000 eV  (added to PSCEN)


Free energy of the ion-electron system (eV)
 ---------------------------------------------------
 alpha Z        PSCENC =         6.24865773
 Ewald energy   TEWEN  =      2594.25031041
 -Hartree energ DENC   =     -3088.11025622
 -exchange      EXHF   =         0.00000000
 -V(xc)+E(xc)   XCENC  =        55.11388191
 PAW double counting   =      1719.67695615    -1722.38329519
 entropy T*S    EENTRO =         0.00000000
 eigenvalues    EBANDS =      -190.21985361
 atomic energy  EATOM  =       588.50889549
 Solvation  Ediel_sol  =         0.00000000
 ---------------------------------------------------
 free energy    TOTEN  =       -36.91470334 eV

 energy without entropy =      -36.91470334  energy(sigma->0) =      -36.91470334

Electric field $\mathscr{E}_\text{field}=0.2/\text{Å}$:

DIPCOR: dipole corrections for dipol
direction  3 min pos     1,
dipolmoment           0.000000      0.000000      0.024143 electrons x Angstroem
Tr[quadrupol]       -30.698904

energy correction for charged system         0.000000 eV
dipol+quadrupol energy correction           -0.000251 eV
added-field ion interaction          0.000000 eV  (added to PSCEN)


Free energy of the ion-electron system (eV)
 ---------------------------------------------------
 alpha Z        PSCENC =         6.24840700
 Ewald energy   TEWEN  =      2594.25031041
 -Hartree energ DENC   =     -3088.09457596
 -exchange      EXHF   =         0.00000000
 -V(xc)+E(xc)   XCENC  =        55.11360264
 PAW double counting   =      1719.64714009    -1722.35346620
 entropy T*S    EENTRO =         0.00000000
 eigenvalues    EBANDS =      -190.23743061
 atomic energy  EATOM  =       588.50889549
 Solvation  Ediel_sol  =         0.00000000
 ---------------------------------------------------
 free energy    TOTEN  =       -36.91711714 eV

 energy without entropy =      -36.91711714  energy(sigma->0) =      -36.91711714

Difference in energy ( $E_\text{no-field}-E_\text{add-field}$ ):

 ---------------------------------------------------
 alpha Z        PSCENC =     0.00025073
 Ewald energy   TEWEN  =     0.00000000
 -Hartree energ DENC   =    -0.01568026
 -exchange      EXHF   =     0.00000000
 -V(xc)+E(xc)   XCENC  =     0.00027927
 PAW double counting   =     0.02981606	-0.02982899
 entropy T*S    EENTRO =     0.00000000
 eigenvalues    EBANDS =     0.01757700
 atomic energy  EATOM  =     0.00000000
 Solvation  Ediel_sol  =     0.00000000
 ---------------------------------------------------
 free energy    TOTEN  =       0.00241381 eV

The difference mainly arises from the double counting Hartree energy(See link) and the Kohn-Sham eigenvalues.

A potential SOLVE? Others probably have the same problem as I do: link

NOTE: QE also have this problem. Am I missing something? Since this method directly changed the local potential, am now even not sure if these energy are comparable…

~~UPDATE-2019-01-02~~ After discussion with Arash, I was told that the normal SCF step does not take electric field-dipole interaction into consideration. To fix this, we have to convert the total energy into an enthalpy function by adding the electric field-dipole interaction term:

~~$E_{total}=E_{scf}-dipole*E_{field}$~~

~~Using a convient script , I obtained the result below.~~

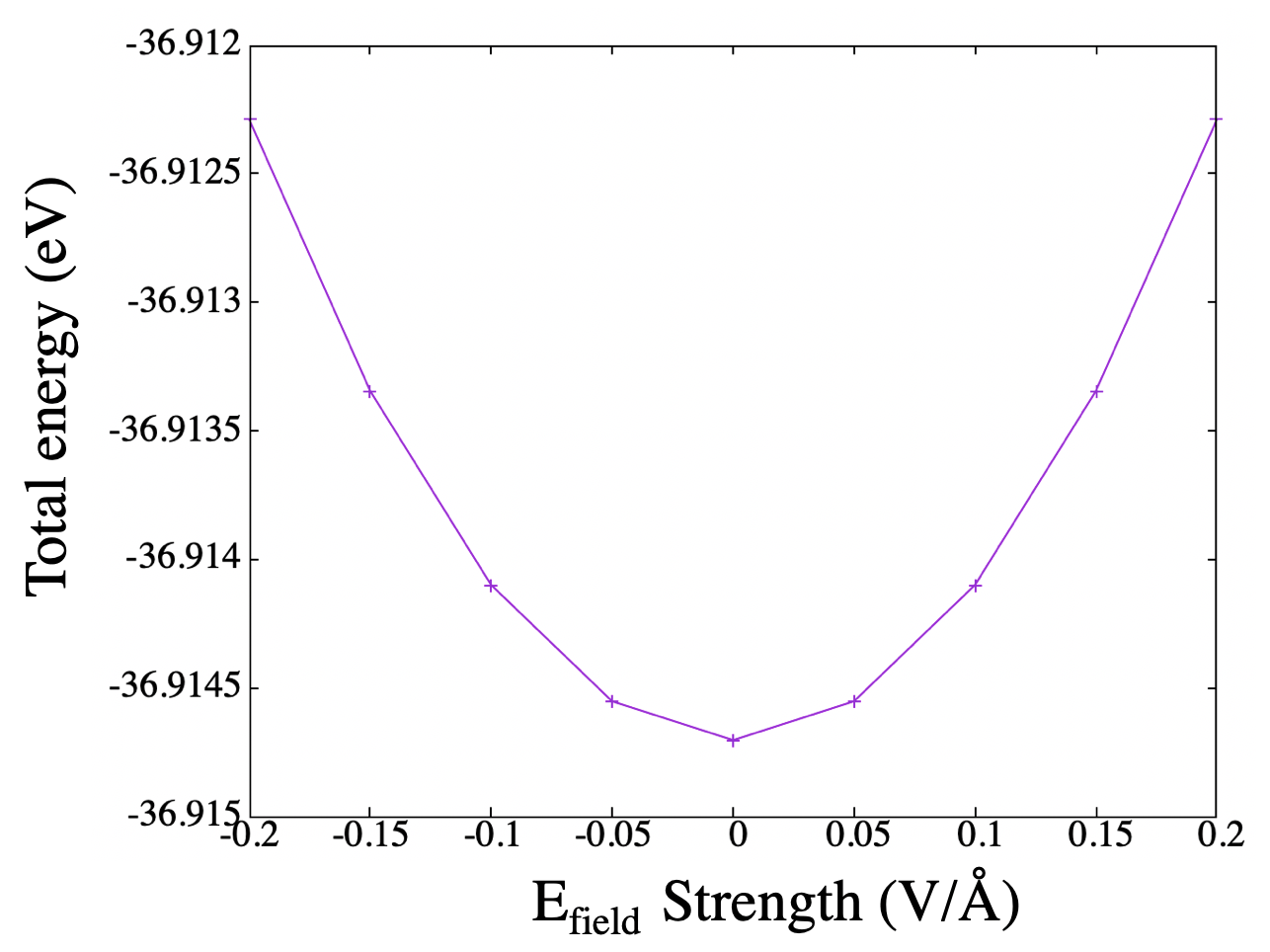
~~All is well now. Phew.~~

UPDATE-2020-03-15 After some more digging:

The main difficulty is the nature of the scalar potential ‘-E*r’, which is nonperiodic and unbounded from below. The nonperiodicity of the potential means that methods based on Bloch’s theorem do not apply. As a result of its unboundedness, the energy can always be lowered by transferring charge from the valence states in one region to conduction states in a distant region.

Ref: 10.1103/PhysRevLett.89.117602

Input

I’ve put all input file in a zip file for download: VASP.